4  Model Analysis

4.1 Load model and data

Code 
# Load random forest model
rf       <- readRDS(here::here("data/rf_for_pH0-10.rds"))
data_cal <- readRDS(here::here("data/cal_for_ph0-10.rds"))
data_val <- readRDS(here::here("data/val_for_ph0-10.rds"))

Our target area to predict over is defined in the file area_to_be_mapped.tif. Since we only want to predict on a given study area, the TIF file comes with a labeling of 0 for pixels that are outside the area of interest and 1 for pixels within the area of interest.

Code 
# Load area to be predicted
target_raster <- terra::rast(here::here("data-raw/geodata/study_area/area_to_be_mapped.tif"))

# Turn target raster into a dataframe, 1 px = 1 cell
target_df <- as.data.frame(target_raster, xy = TRUE)

# Filter only for area of interest
target_df <- target_df |> dplyr::filter(area_to_be_mapped == 1)

# Display df
head(target_df) |> knitr::kable()
x y area_to_be_mapped
2587670 1219750 1
2587690 1219750 1
2587090 1219190 1
2587090 1219170 1
2587110 1219170 1
2587070 1219150 1

Next, we have to load the relevant covariates to run our model:

Warning

Our basic RandomForest model has not undergone any variable selection, so we are loading almost 100 covariates here. However, as discussed during the model training step, it is not sensible to use all covariates at hand.

Code 
# Get a list of all covariate file names
covariate_files <- 
  list.files(path = here::here("data-raw/geodata/covariates/"), 
             pattern = ".tif$",
             recursive = TRUE, 
             full.names = TRUE
             )

# Filter that list only for the variables used in the RF
used_cov <- rf$forest$independent.variable.names
cov_to_load <- c()

for (i_var in used_cov) {
  i <- covariate_files[stringr::str_detect(covariate_files, 
                                           paste0("/", i_var, ".tif"))]
  cov_to_load <- append(cov_to_load, i)
  
  # cat("\nfor var ", i_var, " load file: ", i)
}

# Load all rasters as a stack
cov_raster <- terra::rast(cov_to_load)

# Get coordinates for which we want data
sampling_xy <- target_df |> dplyr::select(x, y)

# Extract data from covariate raster stack
cov_df <-
  terra::extract(cov_raster,  # The raster we want to extract from
                 sampling_xy,  # A matrix of x and y values to extract for
                 ID = FALSE    # To not add a default ID column to the output
                 )

cov_df <- cbind(sampling_xy, cov_df)
Code 
# Attaching reference timeset levels from prepared dataset
bern_cov <- readRDS(here::here("data/bern_sampling_locations_with_covariates.rds"))

cov_df$timeset <- "d1979_2010"
levels(cov_df$timeset) <- c(unique(bern_cov$timeset))

# Define numerically variables 
cat_vars <- 
  cov_df |> 
  # Get number of distinct values per variable
  dplyr::summarise(dplyr::across(dplyr::everything(), ~ dplyr::n_distinct(.))) |> 
  # Turn df into long format for easy filtering
  tidyr::pivot_longer(dplyr::everything(), 
                      names_to = "variable", 
                      values_to = "n") |> 
  # Filter out variables with 10 or less distinct values
  dplyr::filter(n <= 10) |>
  # Extract the names of these variables
  dplyr::pull('variable')

# Define categorical variables 
cov_df <- 
  cov_df |> 
  dplyr::mutate(dplyr::across(cat_vars, ~ as.factor(.)))

# Reduce dataframe to hold only rows without any NA values
cov_df <- 
  cov_df |> 
  tidyr::drop_na()

# Display final dataframe
head(cov_df) |> knitr::kable()
x y Se_curvplan2m_fmean_50c Se_tpi_2m_5c Se_e_aspect2m_5c mt_tt_y Se_SCA2m Se_curvprof2m_s60 Se_e_aspect25m Se_curvprof2m_s7 tsc25_18 Se_curv2m_std_50c Se_slope2m_fmean_5c Se_n_aspect2m_5c mrrtf25 Se_slope2m_std_50c Se_curv2m_std_5c timeset
2587670 1219750 -0.0230801 0.3968636 0.0523264 94 22.039053 0.0286316 -0.0730021 -1.1700106 0.4671952 5.627444 8.8745193 0.9984013 0.1075638 4.443856 8.208909 d1979_2010
2587690 1219750 -0.0118661 -0.0899814 0.0261770 94 274.031982 0.0085285 -0.1002210 0.3911650 0.4697721 5.807981 6.7173972 0.9996192 0.1490467 4.420249 2.624915 d1979_2010
2587090 1219190 -0.0454853 -0.0702948 -0.5646210 94 13.665169 -0.0681556 -0.4406129 0.1884064 0.4930030 6.824774 2.3039992 0.8215204 0.5413071 3.948273 6.073048 d1979_2010
2587090 1219170 -0.0903087 0.0145723 -0.6621951 94 14.756312 -0.0861870 -0.5188757 -0.0721385 0.4922101 6.898385 2.2375104 -0.7484674 0.7348465 3.959431 2.127208 d1979_2010
2587110 1219170 -0.0945719 -0.0001643 -0.3129207 94 32.816425 -0.0599516 -0.3097113 -0.0394869 0.4901487 7.503298 1.9259268 -0.9489474 0.8678100 4.539225 2.297817 d1979_2010
2587070 1219150 -0.0908837 0.0065551 -0.5805916 94 3.599204 -0.1039762 -0.3818592 0.0668136 0.4911794 6.921697 0.7394082 -0.8139611 0.8363171 3.804235 1.829110 d1979_2010

4.2 Model testing

To test our model for how well it predicts on data it has not seen before, we first have to load the {ranger} package to load all functionalities to run a Random Forest in the predict() function. Alongside our model, we feed our validation data into the function and set its parallelization settings to use all but one of our computer’s cores.

4.2.1 Make predictions

Code 
# Need to load {ranger} because ranger-object is used in predict()
library(ranger) 

# Make predictions for validation sites
prediction <- 
  predict(rf,                # RF model
          data = data_val,   # Predictor data
          num.threads = parallel::detectCores() - 1)

# Save predictions to validation df
data_val$pred <- prediction$predictions

4.2.2 Model metrics

Now that we have our predictions ready, we can extract standard metrics for a classification problem (see AGDS Chapter 8.2.2).

Code 
# Calculate error
err <- data_val$ph.0.10 - data_val$pred

# Calculate bias
bias <- mean(err, na.rm = T) |> round(2)

# Calculate RMSE
rmse <- sqrt(mean(err, na.rm = T)) |> round(2)

# Calculate R2
r2 <- cor(data_val$ph.0.10, data_val$pred, method = "pearson")^2 |> round(2)

4.2.3 Metric plots

Code 
data_val |> 
  ggplot2::ggplot(ggplot2::aes(x = pred, y = ph.0.10)) +
  ggplot2::geom_point() +
  ggplot2::geom_smooth(method = "lm",
                       color = "tomato") +
  # Add layout
  ggplot2::theme_classic() +
  ggplot2::geom_abline(
    intercept = 0, 
    slope = 1, 
    linetype = "dotted") +
  ggplot2::ylim(5, 7.5) +
  ggplot2::xlim(5, 7.5) +
  ggplot2::labs(
    title = "Predicted vs. Observed soil pH 0-10 cm",
    # subtitle = paste0("Bias = ", bias, ", RMSE = ", rmse, ", R^2 = ", r2),
    subtitle = bquote(paste("Bias = ", .(bias), 
                            ", RMSE = ", .(rmse), 
                            ", R"^2, " = ", .(r2))),
    x = "Predicted",
    y = "Observed"
  )

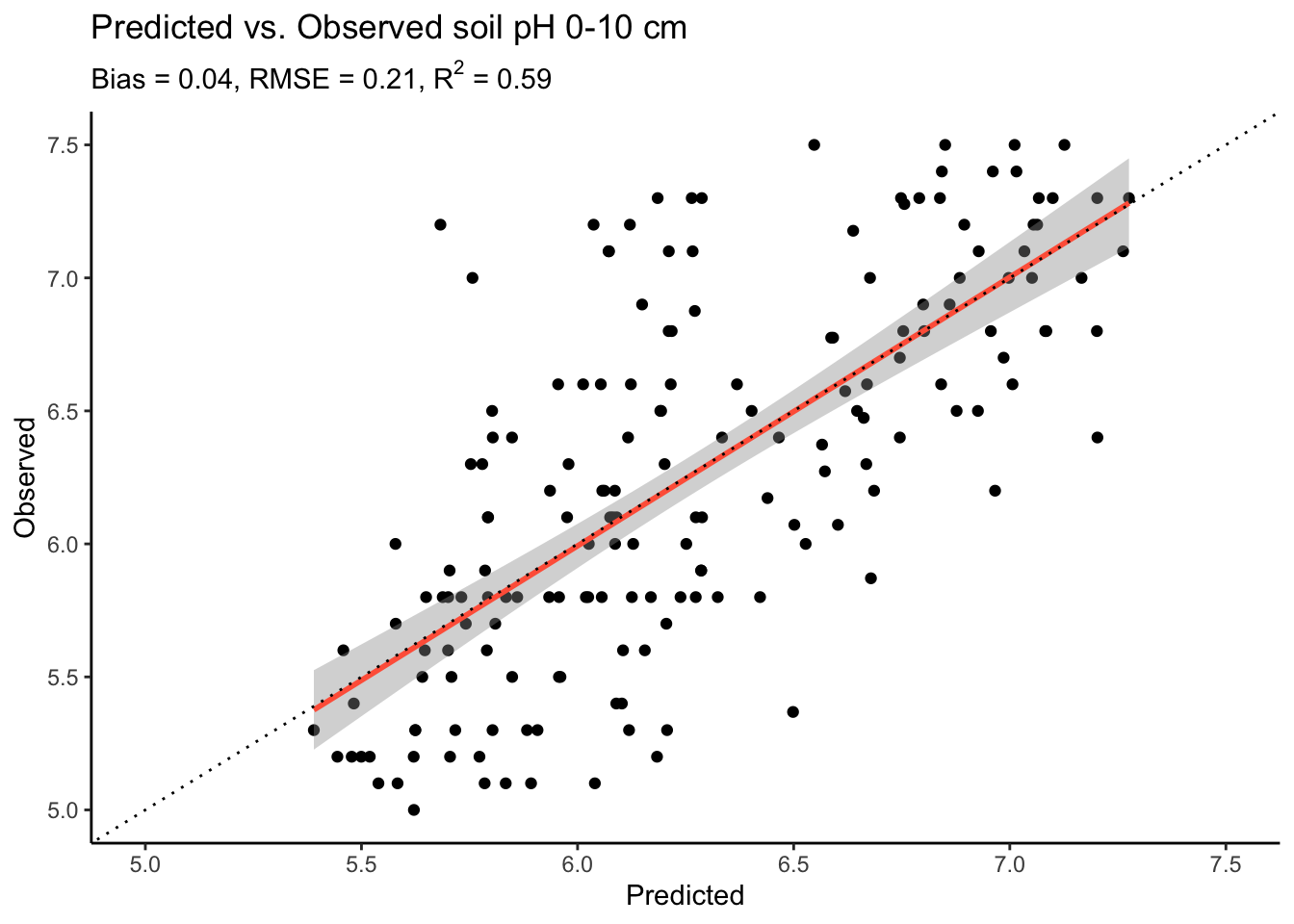
Figure 4.1: Comparison of observed versus predicted values for top soil pH using a simple Random Forest model.

The plot shows that our model performs quite well for the fact that we randomly selected 15 covariates and did no model tuning whatsoever. Yet, we can also see that the model tends to overestimate at low pH values, with quite a bit point cloud to the right of the lower end of the 1:1 line.

4.3 Create prediction maps

Now, we finally come to the probably most interesting part of this tutorial: Creating a map of top soil pH values across our study area. For this, we again make predictions with our Random Forest model but we use our covariates dataframe for the study area, instead of only at the sampling locations as done above.

Code 
# Need to load {ranger} because ranger-object is used in predict()
library(ranger) 

# Make predictions using the RF model
prediction <- 
  predict(rf,              # RF model
          data = cov_df,   # Predictor data
          num.threads = parallel::detectCores() - 1)

# Attach predictions to dataframe and round them
cov_df$prediction <- round(prediction$predictions, 2)
Code 
# Extract dataframe with coordinates and predictions
df_map <- cov_df |> dplyr::select(x, y, prediction)

# Turn dataframe into a raster
ra_predictions <- 
  terra::rast(
    df_map,                  # Table to be transformed
    crs = "+init=epsg:2056", # Swiss coordinate system
    extent = terra::ext(cov_raster) # Prescribe same extent as predictor rasters
            )
Code 
# Let's have a look at our predictions!
# To have some more flexibility, we can plot this in the ggplot-style as such:
ggplot2::ggplot() +
  tidyterra::geom_spatraster(data = ra_predictions) +
  ggplot2::scale_fill_viridis_c(
    na.value = NA,
    option = "viridis",
    name = "pH"
    ) +
  ggplot2::theme_classic() +
  ggplot2::scale_x_continuous(expand = c(0, 0)) +
  ggplot2::scale_y_continuous(expand = c(0, 0)) +
  ggplot2::labs(title = "Predicted soil pH (0 - 10cm)")

Figure 4.2: Predicted map of top soil pH using a simple Random Forest model.

Interesting, we see that our prediction map does not cover the entire study area. This could be a consequence of using a limited set of covariates for our predictions. Moreover, we see that in this study area, there is a tendency of having more acidic soils towards the south west and more basic soils towards the north east. To interpret this map further, we could map it onto a leaflet map, such as done in Chapter 2.

Code 
# Save raster as .tif file
terra::writeRaster(
  ra_predictions,
  "../data/ra_predicted_ph0-10.tif",
  datatype = "FLT4S",  # FLT4S for floats, INT1U for integers (smaller file)
  filetype = "GTiff",  # GeoTiff format
  overwrite = TRUE     # Overwrite existing file
)

4.4 Example for predicting a categorical variable

Below is an example for how you conducted everything you learned in this tutorial, from data wrangling to model evaluation, but with using a categorical response instead of a continuous one.

4.4.1 Data preparation

Code 
# Load clean data
data_clean <- readRDS(here::here("data/bern_sampling_locations_with_covariates.rds"))

# Specify response and predictors
response <- "waterlog.30" # Pick water status at 30cm

# Make sure that response is encoded as factor!
data_clean[[response]] <- factor(data_clean[[response]],
                                 levels = c(0, 1),
                                 labels = c("dry", "wet"))

cat("Target is encoded so that a model predicts the probability that the soil at 30cm is: ",
    levels(data_clean[[response]])[1])
Target is encoded so that a model predicts the probability that the soil at 30cm is:  dry
Code 
# Specify predictors: Remove soil sampling information
predictors <- 
  data_clean |> 
  dplyr::select(-response,                        # Remove response variable
                -site_id_unique,                  # Remove site ID
                -tidyr::starts_with("ph"),        # Remove pH information
                -tidyr::starts_with("waterlog"),  # Remove water-status info
                -dclass,                          # Remove water-status info
                -dataset) |>                      # Remove calib./valid. info
  names()

# Split dataset into calibration and validation
data_cal <- data_clean |> dplyr::filter(dataset == "calibration")
data_val <- data_clean |> dplyr::filter(dataset == "validation")

# Filter out any NA to avoid error when running a Random Forest
data_cal <- data_cal |> tidyr::drop_na()
data_val <- data_val |> tidyr::drop_na()

# A little bit of verbose output:
n_tot <- nrow(data_cal) + nrow(data_val)

perc_cal <- (nrow(data_cal) / n_tot) |> round(2) * 100
perc_val <- (nrow(data_val) / n_tot) |> round(2) * 100

cat("For model training, we have a calibration / validation split of: ",
    perc_cal, "/", perc_val, "%")
For model training, we have a calibration / validation split of:  75 / 25 %

4.4.2 Model training

Code 
rf <- ranger::ranger( 
  y = data_cal[, response],   # Response variable
  x = data_cal[, predictors], # Predictor variables
  probability = TRUE,         # Set true for categorical variable
  seed = 42,                  # Seed to reproduce randomness
  num.threads = parallel::detectCores() - 1) # Use all but one CPU
Warning

Note that we are skipping model interpretation here to keep it brief.

4.4.3 Model testing

4.4.3.1 Model predictions

Code 
# Need to load {ranger} because ranger-object is used in predict()
library(ranger)

# Make predictions for validation sites
prediction <- 
  predict(rf,                # RF model
          data = data_val,   # Predictor data
          num.threads = parallel::detectCores() - 1)

# Save predictions to validation df
# First row holds probability for reference level
data_val$pred <- round(prediction$predictions[, 1], 2)

4.4.3.2 Model metrics

For our predictions, we now have a probabilities for the reference level of our response. To turn this into the original factor levels of 0 and 1, we have to map a threshold to these probabilities. Here, we use a threshold of 50%, which may or may not be optimal - a discussion for another course.

Code 
# Set threshold
thresh <- 0.5

# Translate probability values into comparable factor levels
data_val$pred_lvl <- 
  factor(
    data_val$pred > thresh, 
    levels = c(TRUE, FALSE), 
    labels = levels(data_val[[response]])
    )

Due to the response variable being a categorical variable, we have to use slightly different model metrics to evaluate our model. To get started, we need a confusion matrix. This 2x2 matrix shows all model predictions and whether they were true/false positives/negatives. Have a look at the table printed below. You can see that in the top left cell, 184 predictions for dry sites and 2 predictinos for wet sites were correct. However, our model predicted 12 times that a site would be wet although it was dry, and 2 times that the site was wet when it was dry instead.

Code 
# Create confusion matrix
ma_conf <- 
  table(
    predicted = data_val[[response]],
    observed  = data_val$pred_lvl
  )

# Display confusion matrix
ma_conf 
         observed
predicted dry wet
      dry 185   1
      wet  12   2

From these predictions, we can calculate many different metrics and the {verification} package provides a nice short-cut to get them. Depending on your requirements that your model should meet, you want to investigate different metrics. Here, we will have a look at some more general ones:

Code 
# Compute statistics
l_stat <- verification::multi.cont(ma_conf) 

# Print output
cat(
  "The model showed:",
  "\n a percentage of correct values of: ", l_stat$pc,
  "\n a bias of (dry / wet predictions): ", round(l_stat$bias, 2),
  "\n a Peirce Skill Score of: ", round(l_stat$ps, 2))
The model showed: 
 a percentage of correct values of:  0.935 
 a bias of (dry / wet predictions):  0.94 4.67 
 a Peirce Skill Score of:  0.61

These metrics looks quite good! We see that in 93% of all cases, our model predicted the water status of a soil location accurately [(184+2)/(184+12+2+2) = 0.93]. The model showed almost no bias when predicting at dry sites but tends to overestiamte at wet sites (predicted 12 times a site is wet when it was dry). But note that this could also be a consequence of our data being skewed towards many more dry than wet sites.

The Perice Skill Score answers the question of “How well did the forecast separate ‘yes’ events from ‘no’ events”.1 This means how well our model separated dry from wet sites. The score has a range of [-1, 1] where 1 means that there is a perfect distinction, -1 means that the model always gets it wrong (so, simply taking the opposite of the prediction always get it right), and 0 means that the model is no better than guessing randomly. We see that our model has a score of 0.44, which means that is certainly better than just random predictions but - in line with the bias - tends to predict dry sites to be wet.

Note: The Peirce Skill Score is originally from Peirce, C. S., 1884: The numerical measure of the success of pre- dictions. Science, 4, 453–454. But it has been re-discovered several times since, which is why it also often referred to as “Kuipers Skill Score” or “Hanssen-Kuiper Skill Score”, or “True Skill Statistic”.

4.4.3.3 Metric plots

Let’s create a combined violin-box-plot to get a better feeling for our predictions. The plot below visualizes what we already learned from the model metrics. That is, that our model tends to predict dry sites quite well (see how close the median is to 1?) but suffers from a few outliers. If we were to increase the prediction threshold thresh defined above, our model would perform words, as more outliers fall below the threshold. Also, the prediction for wet sites is not very clear as indicated by the relatively even distribution of predicted probabilities, and the median at around 75%.

Code 
data_val |> 
  ggplot2::ggplot() +
  ggplot2::aes(x = waterlog.30, y = pred, fill = waterlog.30) +
  ggplot2::geom_violin() +
  ggplot2::geom_boxplot(width = 0.07) +
  ggplot2::labs(
    title  = "Prediction of Water Status at 30cm",
    y      = "Predicted Probability",
    x      = "Observed Status",
    fill   = "Water\nStatus"
  ) +
  ggplot2::geom_abline(
    intercept = thresh, 
    slope = 0, 
    linetype = "dotted"
    ) +
  ggplot2::ylim(0, 1) +
  ggplot2::theme_classic()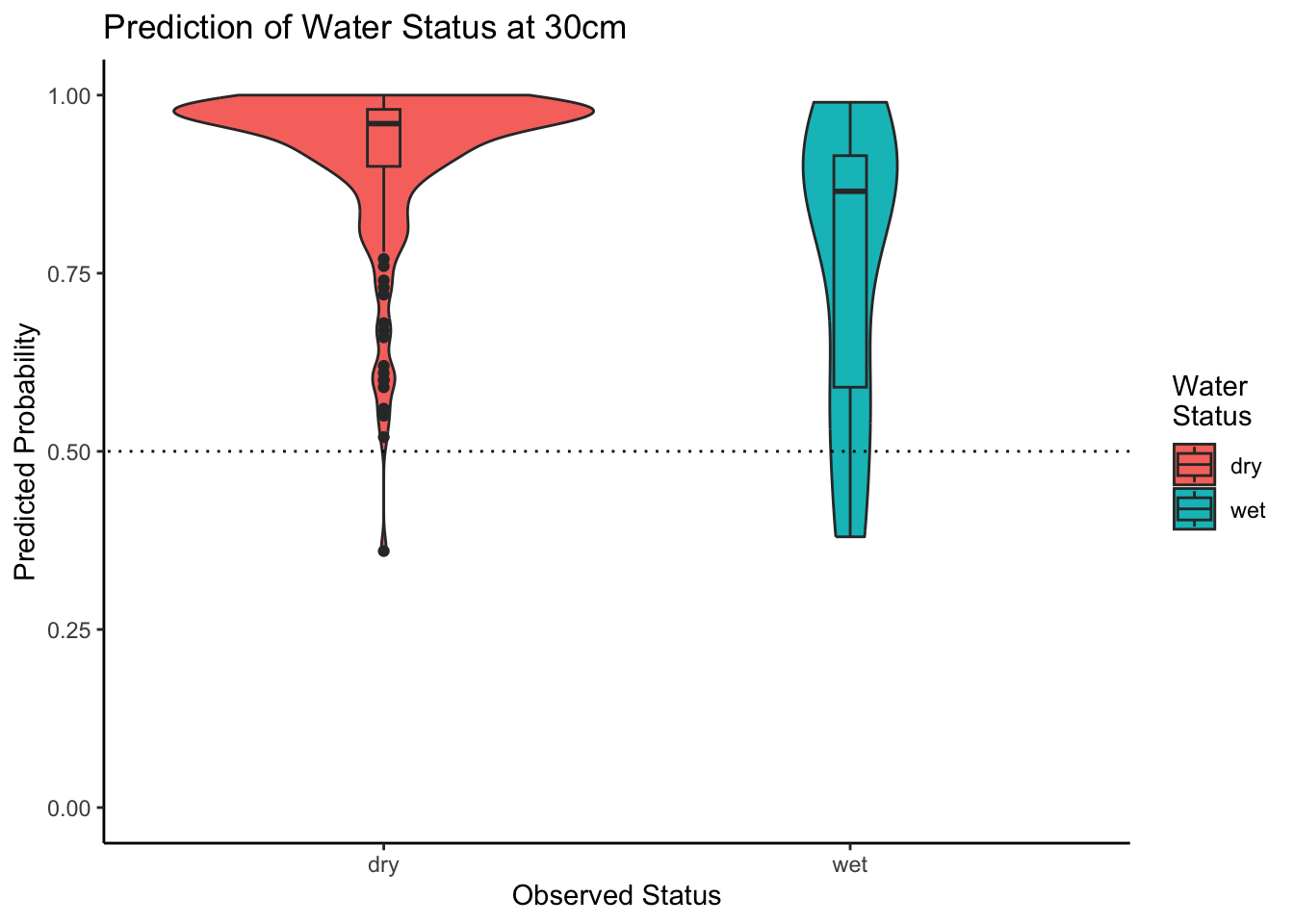

4.4.4 Prediction map

Note that we have not conducted any variable selection for this simplified example. Thus, we have to create a new raster stack with all predictors and cannot re-use the subset that we used for predicting pH.

Code 
# Get a list of all covariate file names
covariate_files <- 
  list.files(path = here::here("data-raw/geodata/covariates/"), 
             pattern = ".tif$",
             recursive = TRUE, 
             full.names = TRUE
             )

# Load all rasters as a stack
cov_raster <- terra::rast(covariate_files)

# Get coordinates for which we want data
sampling_xy <- target_df |> dplyr::select(x, y)

# Extract data from covariate raster stack
cov_df <-
  terra::extract(cov_raster,  # The raster we want to extract from
                 sampling_xy,  # A matrix of x and y values to extract for
                 ID = FALSE    # To not add a default ID column to the output
                 )

cov_df <- cbind(sampling_xy, cov_df)
Code 
# Attaching reference timeset levels from prepared dataset
bern_cov <- readRDS(here::here("data/bern_sampling_locations_with_covariates.rds"))

cov_df$timeset <- "d1979_2010"
levels(cov_df$timeset) <- c(unique(bern_cov$timeset))

# Define numerically encoded categorical variables 
cat_vars <- 
  cov_df |> 
  # Get number of distinct values per variable
  dplyr::summarise(dplyr::across(dplyr::everything(), ~ dplyr::n_distinct(.))) |> 
  # Turn df into long format for easy filtering
  tidyr::pivot_longer(dplyr::everything(), 
                      names_to = "variable", 
                      values_to = "n") |> 
  # Filter out variables with 10 or less distinct values
  dplyr::filter(n <= 10) |>
  # Extract the names of these variables
  dplyr::pull('variable')

cov_df <- 
  cov_df |> 
  dplyr::mutate(dplyr::across(cat_vars, ~ as.factor(.)))

# Reduce dataframe to hold only rows without any NA values
cov_df <- 
  cov_df |> 
  tidyr::drop_na()

# Display final dataframe
head(cov_df) |> knitr::kable()
x y be_gwn25_hdist be_gwn25_vdist cindx10_25 cindx50_25 geo500h1id geo500h3id lgm lsf mrrtf25 mrvbf25 mt_gh_y mt_rr_y mt_td_y mt_tt_y mt_ttvar NegO PosO protindx Se_alti2m_std_50c Se_conv2m Se_curv25m Se_curv2m_fmean_50c Se_curv2m_fmean_5c Se_curv2m_s60 Se_curv2m_std_50c Se_curv2m_std_5c Se_curv2m Se_curv50m Se_curv6m Se_curvplan25m Se_curvplan2m_fmean_50c Se_curvplan2m_fmean_5c Se_curvplan2m_s60 Se_curvplan2m_s7 Se_curvplan2m_std_50c Se_curvplan2m_std_5c Se_curvplan2m Se_curvplan50m Se_curvprof25m Se_curvprof2m_fmean_50c Se_curvprof2m_fmean_5c Se_curvprof2m_s60 Se_curvprof2m_s7 Se_curvprof2m_std_50c Se_curvprof2m_std_5c Se_curvprof2m Se_curvprof50m Se_diss2m_50c Se_diss2m_5c Se_e_aspect25m Se_e_aspect2m_5c Se_e_aspect2m Se_e_aspect50m Se_MRRTF2m Se_MRVBF2m Se_n_aspect2m_50c Se_n_aspect2m_5c Se_n_aspect2m Se_n_aspect50m Se_n_aspect6m Se_NO2m_r500 Se_PO2m_r500 Se_rough2m_10c Se_rough2m_5c Se_rough2m_rect3c Se_SAR2m Se_SCA2m Se_slope2m_fmean_50c Se_slope2m_fmean_5c Se_slope2m_s60 Se_slope2m_s7 Se_slope2m_std_50c Se_slope2m_std_5c Se_slope2m Se_slope50m Se_slope6m Se_toposcale2m_r3_r50_i10s Se_tpi_2m_50c Se_tpi_2m_5c Se_tri2m_altern_3c Se_tsc10_2m Se_TWI2m_s15 Se_TWI2m_s60 Se_TWI2m Se_vrm2m_r10c Se_vrm2m terrTextur tsc25_18 tsc25_40 vdcn25 vszone timeset
2587670 1219750 852.6916 15.664033 -1.093336 9.219586 5 0 6 1.6357950 0.1075638 0.7211104 1311.320 10791.72 57 94 183 1.526693 1.475333 0.0650055 4.784680 5.095301 -0.1573657 0.0024712 0.8294562 -0.0401642 5.627444 8.208909 5.1277814 -0.0951815 2.5569961 -0.0534006 -0.0230801 0.1763837 -0.0115326 0.3709164 2.520638 3.900391 1.0937366 -0.0541850 0.1039651 -0.0255513 -0.6530724 0.0286316 -1.1700106 4.067357 5.008852 -4.0340447 0.0409964 0.3920868 0.7319978 -0.0730021 0.0523264 0.1118718 -0.0341700 0.2049596 0.2460670 0.9587829 0.9984013 0.9855098 0.9959861 0.9919792 1.453115 1.499916 1.2614983 0.9052418 0.4487450 4.031501 22.039053 5.379811 8.8745193 6.507652 8.9208927 4.443856 4.4604211 6.7506914 5.657930 9.0587664 0 -0.1146867 0.3968636 23.013111 0.4660870 0.0196044 0.0193961 0.0094032 0.0049250 0.0021733 0.4892213 0.4671952 2.447572 32.42764 5 d1979_2010
2587690 1219750 842.4173 14.940482 -1.088761 8.887812 5 0 6 1.6952833 0.1490467 0.6501970 1311.240 10790.04 57 94 183 1.519305 1.479355 0.0614093 4.554082 -1.164458 -0.0033177 0.0346522 -0.2036149 -0.0067883 5.807981 2.624915 0.0343211 -0.0114668 -0.5821388 0.0590281 -0.0118661 0.0516823 0.0017402 -0.1523290 2.609372 1.747575 -0.0235629 -0.0044247 0.0623458 -0.0465183 0.2552971 0.0085285 0.3911650 4.186157 1.268572 -0.0578840 0.0070421 0.3616736 0.4156418 -0.1002210 0.0261770 0.1186721 -0.0198933 0.1900981 0.4769361 0.9681105 0.9996192 0.9919428 0.9949375 0.9969665 1.509942 1.481037 1.1013201 0.7694993 0.4196114 4.022690 274.031982 5.293089 6.7173972 6.291715 6.6285639 4.420249 1.4163034 6.0838585 5.312412 6.6105819 0 -0.5947826 -0.0899814 20.897743 0.4708194 0.0147714 0.0177614 0.0012333 0.0016250 0.0001495 0.4985980 0.4697721 2.450347 32.34033 5 d1979_2010
2587090 1219190 751.8956 5.726926 -11.884583 -11.109116 4 0 6 0.5349063 0.5413071 1.4682430 1310.274 10723.66 58 94 184 1.555187 1.503930 0.0460703 1.626563 -20.532444 0.0084397 0.0061933 0.0839349 -0.0022937 6.824774 6.073048 -1.7545626 -0.0072457 -1.0616286 -0.0088943 -0.0454853 0.0885931 -0.0704493 0.1036513 2.366981 1.279673 1.0475039 -0.0017489 -0.0173340 -0.0516786 0.0046582 -0.0681556 0.1884064 5.534662 5.491115 2.8020666 0.0054969 0.5250703 0.3176954 -0.4406129 -0.5646210 -0.0504419 -0.2286900 0.0928654 1.1235304 -0.9772032 0.8215204 0.9954001 -0.9600990 0.9919993 1.515766 1.494511 0.5166996 0.4931896 0.4272473 4.022115 13.665169 3.551755 2.3039992 3.040830 2.7184446 3.948273 2.3797400 5.7317319 1.395017 2.3336451 0 -0.0982406 -0.0702948 20.768515 0.5078870 0.0197626 0.0162485 0.0259366 0.0020749 0.0012587 0.7806686 0.4930030 2.233182 15.32439 8 d1979_2010
2587090 1219170 735.4257 5.784212 -13.546880 -12.143552 4 0 6 0.5427678 0.7348465 1.4188210 1310.245 10721.32 58 94 184 1.555535 1.504260 0.0452300 1.741869 2.745619 0.0117131 -0.0394273 0.1259893 0.0330435 6.898385 2.127208 0.6203362 0.0312720 -0.0710808 0.0096938 -0.0903087 0.0241072 -0.0531435 0.0095001 2.350148 1.199804 0.2795571 0.0035725 -0.0020192 -0.0508814 -0.1018821 -0.0861870 -0.0721385 5.623002 1.172386 -0.3407791 -0.0276995 0.6905439 0.5443047 -0.5188757 -0.6621951 -0.8731300 -0.2571333 1.7519246 1.1301626 -0.9925461 -0.7484674 -0.4839056 -0.9521305 -0.6938887 1.534615 1.545543 0.5673958 0.4292437 0.2561375 4.003264 14.756312 3.531246 2.2375104 3.003023 2.1449676 3.959431 0.7783145 2.3075097 1.400111 1.9295034 0 0.7135532 0.0145723 13.433935 0.5291796 0.0141175 0.0159906 0.0154473 0.0007750 0.0005787 0.7260778 0.4922101 2.229970 15.40787 8 d1979_2010
2587110 1219170 723.9910 6.106696 -13.322203 -12.183930 4 0 6 0.5323660 0.8678100 1.3493569 1310.299 10722.13 58 94 184 1.555655 1.504170 0.0451466 1.808976 -8.940220 0.0324950 -0.0373967 0.1306849 0.0359804 7.503298 2.297817 -0.1434636 0.0834899 -0.1115735 0.0275330 -0.0945719 0.0954700 -0.0239712 0.0538922 2.387497 1.301248 -0.3521201 0.0365431 -0.0049620 -0.0571752 -0.0352149 -0.0599516 -0.0394869 6.239721 1.240976 -0.2086566 -0.0469468 0.6792284 0.5120147 -0.3097113 -0.3129207 -0.2375892 -0.1402488 2.8863275 1.3914874 -0.9945219 -0.9489474 -0.9524035 -0.9798594 -0.9637377 1.536156 1.546788 0.5236238 0.4052551 0.2287366 4.001763 32.816425 3.856629 1.9259268 3.079502 1.8851717 4.539225 0.4211105 1.6905378 1.347915 1.9237802 0 0.9748727 -0.0001643 11.591580 0.5378539 0.0122094 0.0161002 0.0079080 0.0004500 0.0000955 0.7223964 0.4901487 2.229178 15.43506 8 d1979_2010
2587070 1219150 726.0598 5.136146 -14.969542 -13.059101 4 0 6 0.4896232 0.8363171 1.5352163 1310.168 10718.23 58 94 184 1.556895 1.504168 0.0449906 1.885761 -5.564820 0.1670244 -0.0237084 0.0468207 0.0322937 6.921697 1.829110 -0.2251399 0.0651237 0.1595823 0.0051374 -0.0908837 0.1198024 -0.0716825 0.0926395 2.425535 1.074812 -0.0860424 0.0125605 -0.1618870 -0.0671752 0.0729817 -0.1039762 0.0668136 5.548432 0.934908 0.1390975 -0.0525633 0.7167594 0.4836134 -0.3818592 -0.5805916 -0.9587489 -0.2188960 1.1769800 2.5623682 -0.9945219 -0.8139611 -0.1249791 -0.9608662 -0.7394884 1.541335 1.547748 0.4012785 0.2244926 0.1277301 4.000143 3.599204 3.335257 0.7394082 3.145846 0.6904325 3.804235 0.3790899 0.4726965 2.112438 0.4233291 0 0.7557949 0.0065551 6.877132 0.5070984 0.0124573 0.0161766 0.0134654 0.0003000 0.0000463 0.6677173 0.4911794 2.225173 15.57539 8 d1979_2010

Now that we have our predictor raster again, we can make our predictions and plot them.

Code 
# Need to load {ranger} because ranger-object is used in predict()
library(ranger) 

# Make predictions using the RF model
prediction <- 
  predict(rf,              # RF model
          data = cov_df,   # Predictor data
          num.threads = parallel::detectCores() - 1)

# Attach predictions to dataframe and round them
cov_df$prediction <- round(prediction$predictions[,1], 2)
Tip

Note the difference to the regression task before: To access the predicted probabilities, we need to use prediction$predictions[,1].

Code 
# Extract dataframe with coordinates and predictions
df_map <- cov_df |> dplyr::select(x, y, prediction)

# Turn dataframe into a raster
ra_predictions <- 
  terra::rast(
    df_map,                  # Table to be transformed
    crs = "+init=epsg:2056", # Swiss coordinate system
    extent = terra::ext(cov_raster) # Prescribe same extent as predictor rasters
            )
Code 
# Let's have a look at our predictions!
# To have some more flexibility, we can plot this in the ggplot-style as such:
ggplot2::ggplot() +
  tidyterra::geom_spatraster(data = ra_predictions) +
  ggplot2::scale_fill_viridis_c(
    na.value = NA,
    option = "viridis",
    name = "Probability"
    ) +
  ggplot2::theme_classic() +
  ggplot2::scale_x_continuous(expand = c(0, 0)) +
  ggplot2::scale_y_continuous(expand = c(0, 0)) +
  ggplot2::labs(title = expression(paste("Predicted probability for ", 
                                         italic(bold("no")), 
                                         " waterlog at 30 cm")))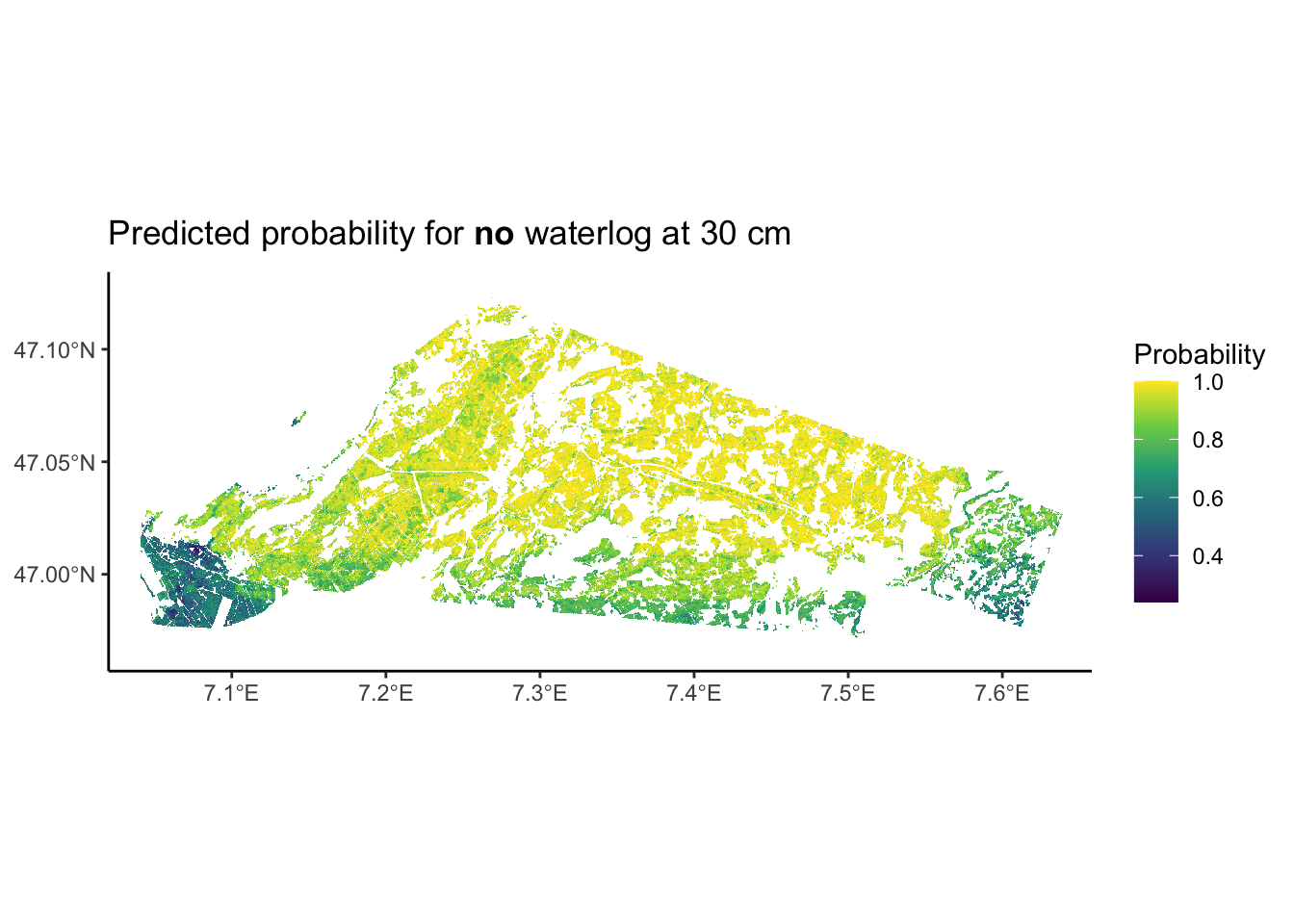

  1. See this useful page on forecast verification: https://www.cawcr.gov.au/projects/verification/↩︎